跳转至

风险模型

作者：Robert Andrew Martin

译者：片刻小哥哥

项目地址：https://www.dafeiyang.cn/finance/stock/tools/PyPortfolioOpt/RiskModels

原始地址：https://pyportfolioopt.readthedocs.io/en/latest/RiskModels.html

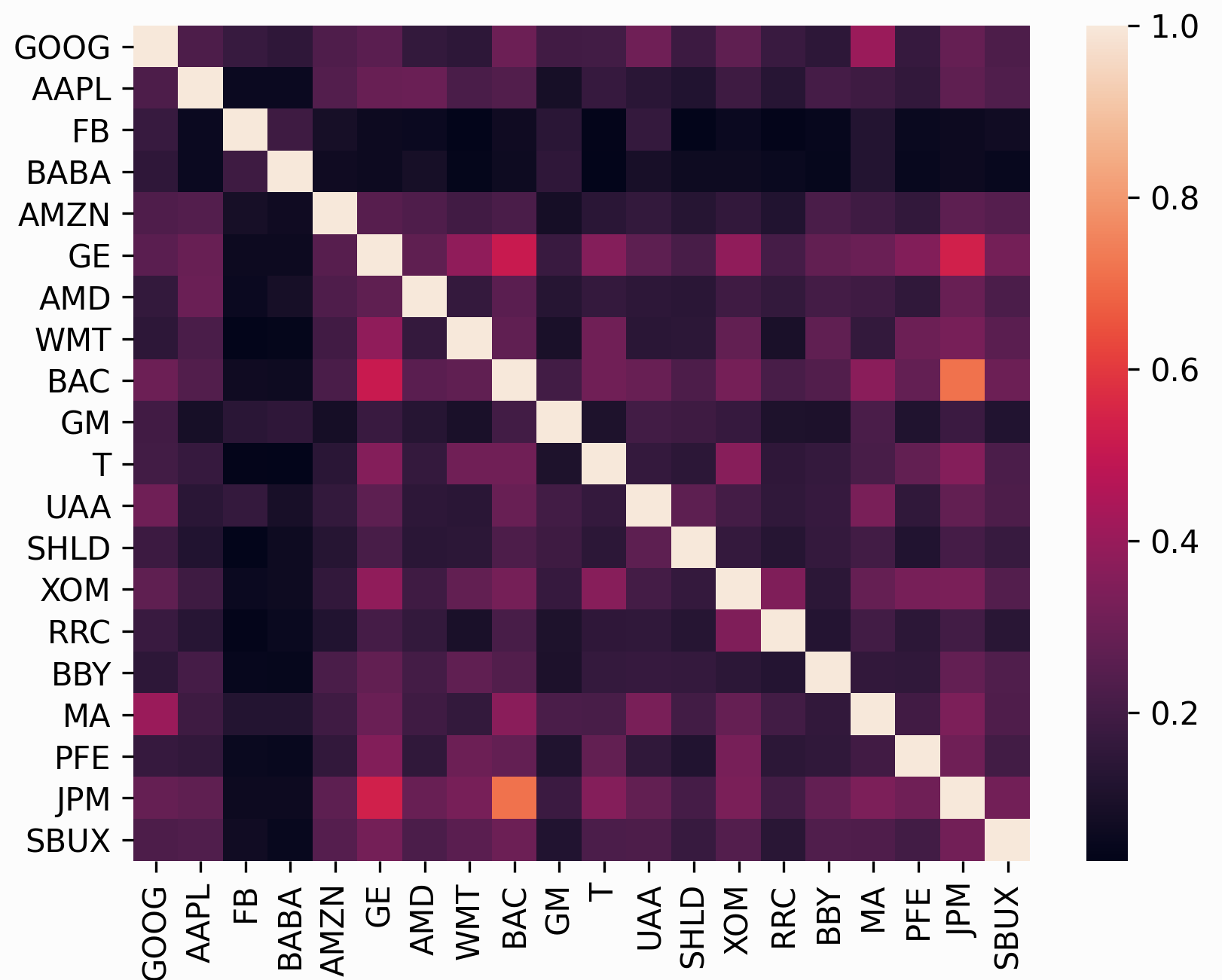
除了预期回报之外，均值方差优化还需要 风险模型 ，某种量化资产风险的方法。最常用的风险模型 是协方差矩阵，描述资产波动性及其相互依赖性。这是 很重要，因为多元化的原则之一是风险可以被 通过进行许多不相关的投注来减少(相关性只是标准化 协方差)。

协方差矩阵图

在许多方面，风险模型的主题比预期收益的主题要重要得多，因为历史方差通常是比平均历史收益更持久的统计数据。 事实上，克里茨曼等人的研究。 (2010) [1] 表明，通过优化而不提供预期回报而形成的最小方差投资组合实际上在样本外表现更好。

然而问题是，在实践中我们无法获得协方差 矩阵(就像我们无法获得预期回报一样)——唯一的 我们能做的就是根据过去的数据进行估计。最直接的 方法是只计算 样本协方差矩阵 基于历史的 回报，但最近(2000 年后)的研究表明，有很多 协方差矩阵的更稳健的统计估计器。此外 为估计器提供一个包装器 sklearn , PyPortfolioOpt 提供了一些实验替代方案，例如半协方差和指数加权协方差。

注意力

协方差矩阵的估计是一个非常深入且研究活跃的主题，涉及统计学、计量经济学和数值/计算方法。 PyPortfolioOpt 实现了多个选项，但还有很大的改进空间。

risk_models 模块提供了根据历史收益估计协方差矩阵的函数。

数据输入的格式与 预期回报 中的相同。

目前实施：

  • 修复非正半定矩阵
  • 通用风险矩阵函数，允许您从一个函数运行任何风险模型。
  • 样本协方差
  • 半协方差
  • 指数加权协方差
  • 最小协方差行列式
  • 缩小协方差矩阵：
  • 手动收缩
  • Ledoit Wolf 收缩
  • Oracle Approximating 收缩
  • 相关矩阵的协方差

笔记

对于任何这些方法，如果您希望传递回报(默认为价格)，设置布尔标志 returns_data=True

pypfopt.risk_models.risk_matrix(prices, method='sample_cov', **kwargs) [来源]

使用中提供的风险模型计算协方差矩阵 method 范围。

Parameters:

  • prices ( pd.DataFrame ) – 调整后的资产收盘价，每行是一个日期 每列都是一个股票代码/id。
  • returns_data ( bool, 默认为 False ) – 如果为真，第一个参数是回报而不是价格。
  • method ( str, optional ) – 要使用的风险模型。应该是以下之一：
  • sample_cov
  • semicovariance
  • exp_cov
  • ledoit_wolf
  • ledoit_wolf_constant_variance
  • ledoit_wolf_single_factor
  • ledoit_wolf_constant_correlation
  • oracle_approximating

Raises: NotImplementedError – 如果提供的方法无法识别

Returns: 年化样本协方差矩阵

Return type: pd.DataFrame

pypfopt.risk_models.fix_nonpositive_semidefinite(matrix, fix_method='spectral') [来源]

检查协方差矩阵是否是半正定的，如果不是，则修复它 使用所选方法。

spectral 方法将负特征值设置为零，然后重建矩阵，而 diag 方法向对角线添加一个小的正值。

Parameters:

  • matrix ( pd.DataFrame ) – 原始协方差矩阵(可能不是 PSD)
  • fix_method ( str, optional ) – {“spectral”, “diag”}，默认为“spectral”

Raises: NotImplementedError – 如果传递了一个未实现的方法

Returns: 正半定协方差矩阵

Return type: pd.DataFrame

并非所有计算的协方差矩阵都是半正定 (PSD) 的。这个方法检查矩阵是否为 PSD，如果不是则修复它。

pypfopt.risk_models.sample_cov(prices, returns_data=False, frequency=252, log_returns=False, **kwargs) [来源]

计算 (daily) 资产回报的年化样本协方差矩阵。

Parameters:

  • prices ( pd.DataFrame ) – 调整后的资产收盘价，每行是一个日期每列都是一个股票代码/id。
  • returns_data ( bool, 默认为 False ) – 如果为真，第一个参数是回报而不是价格。
  • frequency ( int, optional ) – 一年中的时间段数，默认为 252(一年中的交易日数)
  • log_returns ( bool, 默认为 False ) – 是否使用对数返回进行计算

Returns: 年化样本协方差矩阵

Return type: pd.DataFrame

这是教科书默认的方法。 样本协方差矩阵(我们表示为 \(S\))中的条目是第 \(i\) 个资产和第 \(j\) 个资产之间的样本协方差(对角线由方差组成)。 尽管样本协方差矩阵是协方差矩阵的无偏估计，即 \(E(S) = \Sigma\)，但实际上它会遭受错误指定错误和缺乏鲁棒性。 这在均值方差优化中尤其成问题，因为优化器可能会额外相信错误值。

笔记

这不应该是您的默认选择！ 请改用收缩估算器。

pypfopt.risk_models.semicovariance(prices, returns_data=False, benchmark=7.9e-05, frequency=252, log_returns=False, **kwargs) [来源]

估计半协方差矩阵，即协方差给定 回报低于基准。

Parameters:

  • prices ( pd.DataFrame ) – 调整后的资产收盘价，每行是一个日期 每列都是一个股票代码/id。
  • returns_data ( bool, 默认为 False ) – 如果为真，第一个参数是回报而不是价格。
  • benchmark ( float ) – 基准回报率，默认为每日无风险利率，即 \(1.02^{(1/252)} -1\) 。
  • frequency ( int, optional ) – 一年中的时间段数，默认为 252(一年中的交易日数)。确保您使用适当的基准，例如如果 frequency=12 使用每月无风险利率。
  • log_returns ( bool, 默认为 False ) – 是否使用对数返回进行计算

Returns: 半协方差矩阵

Return type: pd.DataFrame

半方差是低于某个基准 \(B\)(通常是无风险利率)的所有回报的方差——它是下行风险的常见衡量标准。 定义半协方差矩阵有多种可能的方法，主要区别在于“成对”性质，即我们是否应该对 \(\min(r_i,B)\min(r_j,B)\) 或 \(\min(r_ir_j, B)\) 求和。 在此实现中，我们遵循了 Estrada (2007) [2] 的建议，首选：

\[ \frac{1}{n}\sum_{i = 1}^n {\sum_{j = 1}^n {\min \left( {{r_i},B} \right)} } \min \left( {{r_j},B} \right) \]

pypfopt.risk_models.exp_cov(prices, returns_data=False, span=180, frequency=252, log_returns=False, **kwargs) [来源]

估计指数加权协方差矩阵，该矩阵为较新的数据赋予更大的权重。

Parameters:

  • prices ( pd.DataFrame ) – 调整后的资产收盘价，每行是一个日期 每列都是一个股票代码/id。
  • returns_data ( bool, 默认为 False ) – 如果为真，第一个参数是回报而不是价格。
  • span ( int, optional ) – 指数加权函数的跨度，默认为 180
  • frequency ( int, optional ) – 一年中的时间段数，默认为 252( 一年中的交易日数)
  • log_returns ( bool, 默认为 False ) – 是否使用对数返回进行计算

Returns: 指数协方差矩阵的年化估计

Return type: pd.DataFrame

指数协方差矩阵是一种在计算协方差时给予最新数据更多权重的新颖方法，就像指数移动平均价格通常优于简单平均价格一样。 有关此估计器如何工作的完整说明，请参阅我的学术网站上的 博客文章。

pypfopt.risk_models.cov_to_corr(cov_matrix) [来源]

将协方差矩阵转换为相关矩阵。

Parameters: cov_matrix ( pd.DataFrame ) – 协方差矩阵

Returns: 相关矩阵

Return type: pd.DataFrame

pypfopt.risk_models.corr_to_cov(corr_matrix, stdevs) [来源]

将相关矩阵转换为协方差矩阵

Parameters:

  • corr_matrix ( pd.DataFrame ) – 相关矩阵
  • stdevs ( 类似 array ) – 标准差向量

Returns: 协方差矩阵

Return type: pd.DataFrame

收缩估算器

对于那些有兴趣了解收缩估计器的人来说，一个很好的起点是 “Ledoit 和 Wolf 的 Honey, I Shrunk the Sample Covariance Matrix [3]”，它很好地捕捉了它们背后的直觉——我们将采用其中使用的符号。 我写了这篇文章的摘要，可以在 我的网站 上找到。 更严格的参考文献可以在 Ledoit 和 Wolf (2001) [4] 中找到。

基本思想是，可以使用以下公式(其中 \(\delta\) 是收缩常数)将无偏但通常估计不佳的样本协方差与结构化估计器 \(𝐹\) 结合起来：

\[ \hat{\Sigma} = \delta F + (1-\delta) S \]

之所以称为收缩(shrinking)，是因为它可以被认为是“收缩(shrinking)”样本 另一个估计量的协方差矩阵，相应地称为 收缩目标(shrinkage target) 。 收缩目标可能存在较大偏差，但估计误差很小。 目标有多种可能的选择，每一种都会产生不同的最佳收缩常数 \(\delta\)。 PyPortfolioOpt 提供以下收缩方法：：

  • Ledoit-Wolf 收缩率：
  • constant_variance 收缩，即目标是对角矩阵，对角线上是资产方差的平均值，其他地方为零。 这是 sklearn.LedoitWolf 提供的收缩。
  • single_factor 收缩，基于夏普的单一指数模型，该模型有效地使用股票对市场的贝塔值作为风险模型。 参见 Ledoit 和 Wolf 2001 [4]。
  • constant_correlation 收缩，其中所有成对相关性都设置为平均相关性(样本方差不变)。 参见 Ledoit 和 Wolf 2003 [3]
  • Oracle Approximating 收缩(OAS)，由 Chen 等人发明。 (2010) [5]，当样本为高斯或接近高斯时，其均方误差低于 Ledoit-Wolf 收缩。

提示

对于大多数用例，我只会采用 Ledoit Wolf 收缩法，正如 Quantopian 在其量化金融系列讲座中所推荐的那样。

我的实现是在 xtuanta 的帮助下从 Michael Wolf 的网页 上的 Matlab 代码翻译而来的。

class pypfopt.risk_models.CovarianceShrinkage(prices, returns_data=False, frequency=252, log_returns=False) [来源]

提供计算协方差矩阵收缩估计的方法，使用 样本协方差矩阵并选择结构化估计器作为单位矩阵 乘以平均样本方差。收缩常数可以手动输入， 尽管存在估计最佳值的方法(特别是 Ledoit Wolf)。

实例变量：

  • X - pd.DataFrame(returns)
  • S - np.ndarray(样本协方差矩阵)
  • delta - float(收缩常数)
  • frequency - int

__init__(prices, returns_data=False, frequency=252, log_returns=False) [来源]

Parameters:

  • prices ( pd.DataFrame ) – 调整后的资产收盘价，每行是一个日期，每列是一个股票代码/id。
  • returns_data ( bool, 默认为 False ) – 如果为真，第一个参数是回报而不是价格。
  • frequency ( int, optional ) – 一年中的时间段数，默认为252(一年中的交易日数)
  • log_returns ( bool, 默认为 False ) – 是否使用对数返回进行计算

ledoit_wolf(shrinkage_target='constant_variance') [来源]

计算特定的 Ledoit-Wolf 收缩率估计收缩目标。

Parameters: shrinkage_target ( str, optional ) – 选择收缩目标，constant_variance、single_factor 或 constant_correlation。 默认为 constant_variance。

Raises: NotImplementedError – 如果收缩目标无法识别

Returns: 缩小样本协方差矩阵

Return type: np.ndarray

oracle_approximating() [来源]

计算 Oracle Approximating 收缩估计

Returns: 缩小样本协方差矩阵

Return type: np.ndarray

shrunk_covariance(delta=0.2) [来源]

将样本协方差矩阵缩小为单位矩阵(按平均值缩放) 样本方差)。该方法不估计最佳收缩参数， 它需要手动输入。

Parameters: delta ( float, optional ) – 收缩参数，默认为 0.2。

Returns: 缩小样本协方差矩阵

Return type: np.ndarray

参考文献

回到顶部